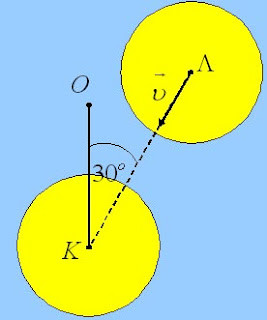
Σε λείο οριζόντιο επίπεδο βρίσκεται ακίνητος δίσκος μάζας 1 kg ακτίνας 0,2
m .
Το κέντρο του είναι συνδεδεμένο μέσω αβαρούς και μη εκτατού νήματος με ακίνητο
σημείο Ο. Η απόσταση ΟΚ είναι ℓ = 0,4
m .
Δεύτερος όμοιος δίσκος κινείται όπως στο σχήμα με ταχύτητα 5
m/s. Η μεταξύ τους κρούση είναι ελαστική
και τριβές δεν αναπτύσσονται μεταξύ των δίσκων.
- Να βρείτε τις τελικές ταχύτητες των δίσκων.
- Τι θα συνέβαινε αν στη θέση του νήματος υπήρχε αβαρής ράβδος η οποία θα επέτρεπε την ελεύθερη ως προς αυτήν περιστροφή του δίσκου;
- Τι θα συνέβαινε αν στη θέση του νήματος υπήρχε αβαρής ράβδος η οποία δεν θα επέτρεπε την ελεύθερη ως προς αυτήν περιστροφή του δίσκου
Θεωρήσατε ότι το τέντωμα δεν προκαλεί θερμικές απώλειες
μηχανικής ενέργειας στο νήμα και στις ράβδους.