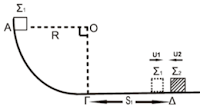
Σώμα Σ, (κύβος) μάζας m=1kg, είναι δεμένο στο κάτω άκρο ιδανικού ελατηρίου σταθεράς k=100N/m.
Το πάνω άκρο του
ελατηρίου είναι στερεωμένο σε ακλόνητο σημείο στην κορυφή κεκλιμένου επιπέδου,
γωνίας κλίσης φ=30ο. Το τμήμα ΒΓ του κεκλιμένου επιπέδου είναι λείο.
Ομογενής κύλινδρος μάζας
Μ=2kg και ακτίνας R=0,1m έχει τυλιγμένο πολλές φορές αβαρές και μη εκτατό νήμα το άλλο άκρο του οποίου
συνδέεται με το σώμα Σ. Ο άξονας του κυλίνδρου είναι οριζόντιος. Το νήμα και ο
άξονας του ελατηρίου βρίσκονται στην ίδια ευθεία, που είναι παράλληλη στο
κεκλιμένο επίπεδο και διέρχεται από το κέντρο μάζας του κύβου. Το σύστημα των
σωμάτων ισορροπεί όπως φαίνεται στο σχήμα 1.
Δ1. Να υπολογίσετε το μέτρο της τάσης
του νήματος και την επιμήκυνση του ελατηρίου
Κάποια στιγμή μετακινούμε τον κύλινδρο κυλώντας τον προς τα κάτω, έτσι ώστε το κέντρο μάζας του να
μετακινηθεί κατά d και την t=0 τον αφήνουμε ελεύθερο να κινηθεί έτσι ώστε να
κυλίεται. Ο κύλινδρος δεν εισέρχεται σε
καμία περίπτωση στο λείο τμήμα ΒΓ του κεκλιμένου επιπέδου. Θεωρείστε θετική φορά την φορά της αρχικής απομάκρυνσης.
Δ2. Να αποδείξετε ότι η μεταφορική κίνηση του κυλίνδρου είναι αρμονική
ταλάντωση με σταθερά επαναφοράς D1 =2Mk/(2m+3M/4).
Δ3. Να υπολογίσετε το μέγιστο επιτρεπτό πλάτος της ταλάντωσης του κυλίνδρου αν
μ=0,5 και το όριο θραύσης Τθ=20Ν.
Δ4.
Να γράψετε την εξίσωση της απομάκρυνσης του σώματος Σ και της γωνιακής
ταχύτητας του κυλίνδρου σε συνάρτηση με το χρόνο αν ο κύλινδρος εκτελεί
ταλάντωση με το μέγιστο δυνατό πλάτος. Συνέχεια εδώ