Αρμονικό
κύμα πλάτους Α διαδίδεται κατά μήκος γραμμικού
ελαστικού μέσου το οποίο ταυτίζεται με το θετικό ημιάξονα Οx. Η πηγή των κυμάτων βρίσκεται στο
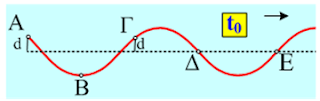
άκρο Ο του ελαστικού μέσου και έχει εξίσωση ταλάντωσης της μορφής y=Aημωt. Μία χρονική στιγμή t1 το στιγμιότυπο του κύματος είναι αυτό του
παραπάνω σχήματος και το σημείο Σ(xΣ=+0,2m) του μέσου ταλαντώνεται
για χρόνο Δt=0,25s.
α) Να βρεθεί η ταχύτητα διάδοσης του κύματος.
β) Να γραφεί η εξίσωση του αρμονικού κύματος.
γ) Να γίνει η γραφική παράσταση της ταχύτητας
ταλάντωσης των σημείων του μέσου σε συνάρτηση με τη συντεταγμένη x για τη
χρονική στιγμή t1.
δ) Κάποια χρονική στιγμή t2, κάποιο σημείο Κ του ελαστικού
μέσου βρίσκεται στη θέση της μέγιστης θετικής απομάκρυνσης yK=+A. Να βρεθεί η
απομάκρυνση που έχει την ίδια στιγμή ένα άλλο σημείο Λ του μέσου με
συντεταγμένη κατά 0,15m μικρότερη
από αυτή του σημείου Κ.
ε) Εάν η γραμμική πυκνότητα του ελαστικού
μέσου είναι μ=80g/m, να βρεθεί η ισχύς της
πηγής του κύματος.