Σάββατο 31 Δεκεμβρίου 2011
Ισορροπία και κίνηση στερεού. Ένα φύλλο εργασίας.
Παρασκευή 30 Δεκεμβρίου 2011
Στάσιμο κύμα
Σε μία χορδή μήκους L=1,5m η οποία είναι δεμένη και στα δύο άκρα της έχει δημιουργηθεί στάσιμο κύμα. Η ταχύτητα διάδοσης των τρέχοντων κυμάτων που από την συμβολή τους δημιουργήθηκε το στάσιμο είναι 12m/s ενώ την χρονική στιγμή t1 όπου η κινητική ενέργεια των υλικών σημείων της χορδής είναι τριπλάσια της δυναμικής ενέργειας ταλάντωσης, η απομάκρυνση ενός σημείου που αντιστοιχεί σε κοιλία είναι yK=+0,1m. Θεωρούμε ως t=0 τη στιγμή που όλα τα μόρια της χορδής διέρχονται από την θέση ισορροπίας τους με αυτά που βρίσκονται πλησιέστερα στο αριστερό άκρο να έχουν u>0.
a) H συχνότητα ταλάντωσης των σωματιδίων του μέσου μπορεί να είναι:
i) 22Hz ii) 20Hz iii) 18Hz
β) Το πλάτος των τρέχοντων κυμάτων που συμβάλλουν είναι
i) 0,05m ii) 0,1m iii) 0,2m
γ) Αν την χρονική στιγμή που τα σωματίδια του μέσου έχουν μηδενική κινητική ενέργεια η απόσταση δύο διαδοχικών κοιλιών είναι d=0,5m, το μήκος κύματος είναι:
i) 0,6m ii) 0,3m iii) 0,25m
δ) Ο αριθμός των δεσμών που σχηματίζονται στην χορδή είναι:
i) 4 ii) 5 iii) 6
ε) Την χρονική στιγμή t= να βρείτε την απομάκρυνση από την θέση ισορροπίας ενός σημείου της χορδής που απέχει 0,4m από το αριστερό της άκρο
Απάντηση:
Μπορούμε να φωτίσουμε το σημείο;
Απάντηση:
Ερώτηση στη Μηχανική στερεού
Άλλο ένα στάσιμο σε χορδή και η εξίσωσή του.
Τετάρτη 28 Δεκεμβρίου 2011

α) Να αποδείξετε ότι το νήμα είναι κατακόρυφο.
β) Να υπολογίσετε την τάση του νήματος.
γ) Κάποια στιγμή κόβουμε το νήμα. Σε πόση απόσταση από το Ο, το άκρο Γ θα ακουμπήσει το δάπεδο;
ΛύσηΣάββατο 24 Δεκεμβρίου 2011
ισορροπία δοκού
Η συνέχεια από Εδώ
Παρασκευή 23 Δεκεμβρίου 2011
μη ομογενής ράβδος και ροπή ζεύγους
Πέμπτη 22 Δεκεμβρίου 2011
Επαναληπτική άσκηση (Κρούσεις-Ταλαντώσεις-Doppler) - Όπως δημιουργήθηκε και αναλύθηκε μέσα στην τάξη
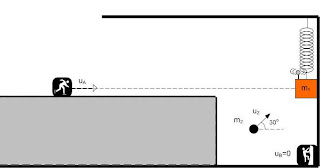
Σώμα μάζας m1=3 kg είναι δεμένο στην άκρη κατακόρυφου ιδανικού ελατήριου σταθεράς k=100 N/m, όπως φαίνεται στο σχήμα, και ισορροπεί. Η μία πλευρά του σώματος m1 βρίσκεται σε επαφή με λεία επιφάνεια τοίχου. Επίσης, στο σώμα μάζας m1 είναι εγκατεστημένη συσκευή παραγωγής ηχητικών κυμάτων συχνότητας fs=680 Hz, η οποία έχει αμελητέα μάζα. Σώμα μάζας m2=1 kg συγκρούεται πλαστικά με το σώμα μάζας m1. Η ταχύτητα του σώματος m2 είναι u2=4∙3^0,5 m/s και το διάνυσμα αυτής σχηματίζει γωνία 30ο με την οριζόντια διεύθυνση. Ως χρονική στιγμή t=0 θεωρείται αυτή της κρούσης.
Επίσης δύο παρατηρητές (Α) και (Β) αντιλαμβάνονται τον ήχο από την πηγή παραγωγής ηχητικών κυμάτων. Ο παρατηρητής (Α) κινείται σε οριζόντιο επίπεδο η προέκταση του οποίου «περνάει» από την αρχική θέση του σώματος μάζας m1. Η ταχύτητα του παρατηρητή (Α) είναι 3 m/s. Ο παρατηρητής (Β) είναι ακίνητος και βρίσκεται στον κατακόρυφο άξονα που διέρχεται από το σώμα μάζας m1.
Δίνεται, επίσης, η επιτάχυνση της βαρύτητας g=10 m/s2 και η ταχύτητα του ήχου uηχ=340 m/s. Θεωρήστε θετική φορά την άνω. Επίσης, μην λάβετε υπόψη τις ανακλάσεις του ήχου.
Να απαντηθούν τα ακόλουθα ζητήματα:
1. Να αποδείξετε ότι το συσσωμάτωμα που θα δημιουργηθεί εκτελεί ΑΑΤ.
2. Να γράψετε την εξίσωση της απομάκρυνσης της ΑΑΤ.
3. Να βρείτε τη μέγιστη τιμή της δύναμης του ελατηρίου και τη μέγιστη τιμή της δύναμης επαναφοράς.
4. Να υπολογιστεί ο χρόνος που απαιτείται ώστε το συσσωμάτωμα να ακινητοποιηθεί ακαριαία για 2η φορά.
5. Να βρεθεί το έργο του βάρους και το έργο της δύναμης ελατηρίου κατά την προαναφερθείσα κίνηση.
6. Σε ποιες χρονικές στιγμές αντιλαμβάνεται ο παρατηρητής (Β) τον ήχο με την ίδια συχνότητα με αυτή που εκπέμπεται από την πηγή.
7. Ποια η συχνότητα που αντιλαμβάνεται ο παρατηρητής (Α) τη στιγμή που το συσσωμάτωμα έχει ταχύτητα 3^0,5/2 m/sμε φορά προς τα κάτω.
8. Να γραφεί η εξίσωση της συχνότητας που αντιλαμβάνεται ο παρατηρητής (Β) σε σχέση με το χρόνο.
Με αφορμή ένα στιγμιότυπο στάσιμου κύματος

- Το μήκος κύματος λ.
- Την ταχύτητα στη θέση x = 0 την χρονική στιγμή t1 .
- Σε πόσο χρόνο ,τα υλικά σημεία της χορδής που ταλαντώνονται, θα σταματήσουν να κινούνται για πρώτη φορά μετά την χρονική στιγμή t1.
- Τα μέτρα των ταχυτήτων στα σημεία που βρίσκονται στις θέσεις x = xk = [(12k+1)/3]·λ/4 , την χρονική στιγμή t1 , όπου k = 0,1,2,3,….
Τετάρτη 21 Δεκεμβρίου 2011
Ροπές σε ένα κωνικό εκκρεμές.
Απάντηση
Συνήθως η απόσταση από την θέση ισορροπίας δεν είναι εύκολο να μετρηθεί
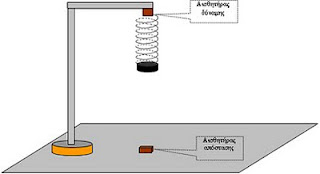 Στην διάταξη του σχήματος εικονίζεται ένα σώμα μάζας m=1Kg, το οποίο ισορροπεί κρεμασμένο στο κάτω άκρο κατακόρυφου ελατηρίου σταθεράς k=100N/m.
Στην διάταξη του σχήματος εικονίζεται ένα σώμα μάζας m=1Kg, το οποίο ισορροπεί κρεμασμένο στο κάτω άκρο κατακόρυφου ελατηρίου σταθεράς k=100N/m.Το άνω άκρο του ελατηρίου είναι στερεωμένο σε ακλόνητο αισθητήρα δύναμης, ο οποίος μετρά την δύναμη που ασκεί το ελατήριο σε αυτόν.
Στην ίδια κατακόρυφο με τον άξονα του ελατηρίου και σε απόσταση d=0,3m από το σώμα βρίσκεται ένας αισθητήρας απόστασης, ο οποίος μετρά την απόσταση του σώματος από αυτόν.
Οι δύο αισθητήρες είναι συνδεδεμένοι με ένα σύστημα multilog, το οποίο μπορεί να καταγράφει τις ενδείξεις των δύο αισθητήρων συναρτήσει του χρόνου.
Ανυψώνουμε το σώμα σε τέτοια θέση ώστε ο αισθητήρας δύναμης να δείχνει μηδέν.
Την στιγμή t=0 αφήνουμε το σώμα ελεύθερο να κινηθεί.
Να υπολογίσετε:
α) Την περίοδο και το πλάτος της ταλάντωσης που θα εκτελέσει το σώμα.
β) Την εξίσωση της απομάκρυνσης του σώματος από την θέση ισορροπίας του συναρτήσει του χρόνου.
γ) Την εξίσωση της απόστασης S του σώματος από τον αισθητήρα απόστασης συναρτήσει του χρόνου.
δ) Την ένδειξη F του αισθητήρα δύναμης συναρτήσει του χρόνου.
ε) Τη σχέση F=g(S) και να την παραστήσετε γραφικά.
στ) Τον χρόνο που απαιτείται μέχρι η επιμήκυνση του ελατηρίου να γίνει ίση με τα ¾ της μεγίστης τιμής της για πρώτη φορά।
Απάντηση σε pdf και σε Word
άσκηση στην ισορροπία στερεού σώματος
Δευτέρα 19 Δεκεμβρίου 2011
Διαγώνισμα στις ταλαντώσεις
Ροπή δύναμης. Φύλλο εργασίας.
ελατήριο και τροχαλία
Κυριακή 18 Δεκεμβρίου 2011
ελατήριο και στερεό σώμα
Σάββατο 17 Δεκεμβρίου 2011
ελατήριο και αρθρωμένη ράβδος
Παρασκευή 16 Δεκεμβρίου 2011
ερώτηση κατανόησης στο στερεό σώμα
Πέμπτη 15 Δεκεμβρίου 2011
Τροχαλία - σώμα - ελατήριο
Δίνουμε μια αρχική ταχύτητα υ0 στο σώμα προς τα δεξιά.
α) Η ταχύτητα του σώματος την στιγμή που η επιμήκυνση του ελατηρίου είναι μέγιστη.
β) Η μέγιστη επιμήκυνση του ελατηρίου
γ) Η ταχύτητα του σώματος και η γωνιακή ταχύτητα της τροχαλίας την στιγμή που το ελατήριο αποκτά ξανά το φυσικό του μήκος.
δ) Υπό ποία συνθήκη το σώμα θα επιστρέψει στην αρχική του θέση;
ε) Αν ικανοποιείται η συνθήκη του ερωτήματος δ, με πόση ταχύτητα θα επιστρέψει το σώμα στην αρχική του θέση;
Τετάρτη 14 Δεκεμβρίου 2011
Δευτέρα 12 Δεκεμβρίου 2011
Κυκλική-Στροφική κίνηση. Ένα φύλλο εργασίας.
Σύνθεση ταλαντωσεων και συμβολή κυμάτων
Συμβολή Vs Σύνθεση ταλαντώσεων
Κυριακή 11 Δεκεμβρίου 2011
Φορά διάδοσης κύματος, ταλαντώσεις και αποστάσεις υλικών σημείων

- Να βρείτε τη φορά διάδοσης του κύματος.
- Να αποδείξετε ότι τα υλικά σημεία που ταλαντώνονται στα σημεία Μ και Β έχουν κάθε χρονική στιγμή ίσες απομακρύνσεις και ίσες ταχύτητες.
- Να βρείτε πόσο απέχει από το Β στην ευθεία (ε) το κοντινότερό του σημείο προς την μεριά το Λ, το οποίο έχει κάθε χρονική στιγμή την ίδια απομάκρυνση και την ίδια ταχύτητα με το Β.
- Να βρείτε την απόσταση μεταξύ των σημείων Μ και Β της ευθείας (ε)
- Να βρείτε την τιμή του Ν1.
- Να γράψετε την εξίσωση απομάκρυνσης χρόνου για την ταλάντωση υλικού σημείου Γ που ξεκινά να ταλαντώνεται 0,15 s πριν αρχίσει η ταλάντωση στο Μ.










