Λίγη εισαγωγική θεωρία πάνω στην κυκλική κίνηση, την οποία είχα αναρτήσει παλιότερα και την οποία επαναφέρω για τους νέους φίλους που ήρθαν στο μεταξύ στην συντροφιά μας.
Τι πρέπει να ξέρει ένας μαθητής πριν αρχίσει να διδάσκεται την Μηχανική στερεού, από την κυκλική κίνηση υλικού σημείου, την οποία διδάχτηκε ή θα έπρεπε να διδαχτεί στην Α΄Λυκείου.
Ένα υλικό σημείο εκτελεί κυκλική κίνηση σε οριζόντιο επίπεδο, με ακτίνα R γύρω από το σημείο Ο, όπως στο σχήμα.
Πώς μπορούμε να μελετήσουμε την κίνηση του υλικού σημείου; Με δύο διαφορετικούς τρόπους:
1) Με χρήση γραμμικών μεγεθών.
Ποια είναι αυτά; Το μήκος του τόξου που διαγράφει σε κάποιο χρονικό διάστημα, o ρυθμός μεταβολής του μήκους του τόξου αυτού, που είναι η ταχύτητα του υλικού σημείου, και ο ρυθμός μεταβολής της ταχύτητάς του, δηλαδή η επιτάχυνσή του.
Αναφερόμενοι λοιπόν στο παραπάνω σχήμα, αν το σώμα σε χρόνο dt μετακινείται από τη θέση Α στην Β διαγράφοντας το τόξο ds, ορίζουμε την ταχύτητά του (που από εδώ και πέρα θα ονομάζουμε γραμμική ταχύτητα) από την σχέση:
Η γραμμική ταχύτητα είναι πάνω στο επίπεδο της κυκλικής τροχιάς, εφαπτόμενη στον κύκλο (πράγμα που σημαίνει κάθετη στην ακτίνα σε κάθε σημείο).
Η ταχύτητα του υλικού σημείου σε μια κυκλική κίνηση μεταβάλλεται ΠΑΝΤΑ. Ακόμη και αν το μέτρο της παραμένει σταθερό θα αλλάζει η κατεύθυνσή της, αφού θα είναι πάντα εφαπτόμενη του κύκλου. Συνεπώς πάντα υπάρχει επιτάχυνση. Ορίζεται από την γνωστή σχέση:
Ενώ η κατεύθυνσή της είναι προς το εσωτερικό μέρος της κυκλικής τροχιάς. Η επιτάχυνση αυτη μεταβάλλει και το μέτρο και την κατεύθυνση της ταχύτητας. Μπορούμε λοιπόν να αναλύσουμε την επιτάχυνση αυτή σε δύο συνιστώσες. Μια στη διεύθυνση της ταχύτητας, η οποία θα μεταβάλλει το μέτρο της ταχύτητας και μια κάθετη στην ταχύτητα με φορά προς το κέντρο του κύκλου, η οποία μεταβάλλει την κατεύθυνση της ταχύτητας.
Η συνιστώσα αε που είναι κάθετη στην ακτίνα ονομάζεται επιτρόχια επιτάχυνση και αν έχει την ίδια κατεύθυνση με την ταχύτητα θα είναι υπεύθυνη για την αύξηση του μέτρου της ταχύτητας (επιταχυνόμενη κίνηση), ενώ αν έχει αντίθετη φορά, θα μειώνει το μέτρο της ταχύτητας (επιβραδυνόμενη κίνηση).
Η συνιστώσα ακ ονομάζεται κεντρομόλος επιτάχυνση το μέτρο της οποίας δίνεται από την εξίσωση:
Να τονίσουμε ότι αυτή ευθύνεται για την αλλαγή στην κατεύθυνση της ταχύτητας, είναι αυτή που κρατά το σώμα σε κυκλική τροχιά.
Είναι προφανές ότι για έχει το σώμα επιτάχυνση, θα πρέπει να δέχεται και αντίστοιχη συνισταμένη δύναμη, σύμφωνα με τον δεύτερο νόμου του Νεύτωνα. Δηλαδή η συνισταμένη θα έχει την κατεύθυνση της επιτάχυνσης και συνεπώς και αυτή θα μπορούσαμε να την αναλύσουμε επίσης σε δύο συνιστώσες, μια εφαπτομενική ΣFε=m·αε και μια προς το κέντρο του κύκλου, την οποία λέμε και κεντρομόλο δύναμη, ΣFR=m·ακ.
2) Με χρήση γωνιακών μεγεθών.
Αν το υλικό μας σημείο μετακινείται από την θέση (Α) στη θέση (Β), η επιβατική ακτίνα (η ακτίνα που δίνει κάθε στιγμή τη θέση του κινητού) διαγράφει την επίκεντρη γωνία dθ. Γνωρίζοντας λοιπόν τη γωνία που διαγράφει το κινητό γνωρίζουμε κάθε στιγμή και την θέση του.
Μπορούμε και εδώ να ορίσουμε τον ρυθμό με τον οποίο μεταβάλλεται η παραπάνω γωνία. Το μέγεθος που προκύπτει ονομάζεται Γωνιακή ταχύτητα. Αυτή είναι κάθετη στο επίπεδο της κυκλικής τροχιάς, στο κέντρο του κύκλου, με φορά που καθορίζεται από τον κανόνα του δεξιού χεριού, όπως στο σχήμα:
Και το μέτρο της οποίας θα είναι:
με μονάδα μέτρησης το 1 rad/s.
Αν μεταβάλλεται η γωνιακή ταχύτητα, τότε ορίζουμε το ρυθμό μεταβολής της, τον οποίο ονομάζουμε γωνιακή επιτάχυνση:
Η γωνιακή επιτάχυνση είναι επίσης κάθετη στο επίπεδο της κυκλικής τροχιάς στο κέντρο του κύκλου, ενώ η φορά της μπορεί να είναι ίδια με την φορά της γωνιακής ταχύτητας (σχ.1) ή αντίθετης φοράς (σχ.2). Στην πρώτη περίπτωση η γωνιακή ταχύτητα του σώματος αυξάνεται (επιταχυνόμενη κίνηση) ενώ στην δεύτερη μειώνεται (επιβραδυνόμενη κίνηση).
3) Πώς συνδέονται τα παραπάνω μεγέθη;
Η επίκεντρη γωνία dθ και το αντίστοιχο μήκος του τόξου στο οποίο βαίνει συνδέονται με την σχέση:
Παρατηρείστε ότι η γωνία είναι αδιάστατο μέγεθος, συνεπώς δεν έχει μονάδες. Καταχρηστικά και για λόγους διευκόλυνσης μετράμε τις γωνίες σε rad, όπου όταν μια επίκεντρη γωνία βαίνει σε τόξο με μήκος ίσο με την ακτίνα του κύκλου, λέμε ότι είναι ίση με 1 ακτίνιο (rad).
Από την (1) και δουλεύοντας με μέτρα παίρνουμε:
Προσέξτε ότι η σχέση (2) συνδέει τα μέτρα της γραμμικής και γωνιακής ταχύτητας. Μην ξεχνάμε ότι τα διανύσματα είναι όπως λέμε ασύμβατα κάθετα. Το ένα οριζόντιο το άλλο κατακόρυφο, χωρίς να περνάνε από το ίδιο σημείο.
Παραγωγίζοντας την εξίσωση (2) παίρνουμε:
Βλέπουμε ότι το dυ/dt είναι ο ρυθμός μεταβολής του μέτρου της γραμμικής ταχύτητας που συνδέεται με την επιτρόχια επιτάχυνση. Προσοχή λοιπόν και η σχέση (3) συνδέει επίσης τα μέτρα της επιτρόχιας και της γωνικής επιτάχυνσης.
4) Δύο εύκολες κυκλικές κινήσεις.
Α) Ομαλή κυκλική κίνηση:
Αν το υλικό μας σημείο στρέφεται με ταχύτητα σταθερού μέτρου, τότε η κίνηση ονομάζεται ομαλή κυκλική κίνηση. Αλλά τότε δεν θα υπάρχει επιτρόχια επιτάχυνση και θα μπορούσαμε να γράψουμε:
Δs= υ·Δt και αν t0=0 και s0=0 θα είχαμε s=υ·t
Ή αναφερόμενοι σε γωνιακά μεγέθη, αφού η γραμμική ταχύτητα έχει σταθερό μέτρο, από την σχέση (2) προκύπτει ότι και το μέτρο της γωνιακής ταχύτητας παραμένει σταθερό, οπότε αντίστοιχα θα έχουμε:
Δθ=ω·Δt και αν t0=0 και θ0=0 θα είχαμε και θ=ωt (σας θυμίζει τίποτα;).
Β) Ομαλά μεταβαλλόμενη κυκλική κίνηση:
Αν ο ρυθμός μεταβολής της γραμμικής ταχύτητας είναι σταθερός, δηλαδή αε=σταθερή και η γωνιακή επιτάχυνση είναι σταθερή, όπως προκύπτει από τη σχέση (3) και η κίνηση θα είναι είτε κυκλική ομαλά επιταχυνόμενη, είτε κυκλική ομαλά επιβραδυνόμενη και τότε:
Για τα γραμμικά μεγέθη θα ισχύουν οι γνωστές μας σχέσει για το μέτρο της ταχύτητας και για το μήκος του διανυόμενου τόξου:
υ= υ0 ± αε·t και Δs = υ0·t ± ½ αε·t2.
Ενώ όσον αφορά τα γωνιακά μεγέθη θα έχουμε:
ω=ω0 ± αγων·Δt και αν t0=0 θα έχουμε:
ω = ω0 ± αγων·t ( 4)
Αν τέλος κάνουμε τη γραφική παράσταση της γωνιακής ταχύτητας σε συνάρτηση με το χρόνο (για την επιταχυνόμενη κίνηση) παίρνουμε το παρακάτω διάγραμμα:
όπου το εμβαδόν του γκριζαρισμένου τραπεζίου είναι αριθμητική ίσο με την γωνία:


















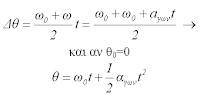
Δεν υπάρχουν σχόλια:
Δημοσίευση σχολίου
Σημείωση: Μόνο ένα μέλος αυτού του ιστολογίου μπορεί να αναρτήσει σχόλιο.